Systèmes du deuxième ordre
Réponse fréquentielle de Bode
\(H(p)={\frac{K}{1+\frac{2z}{\omega _0}p+\frac{p^2}{\omega _0^2}}}\)
ω0 est la pulsation naturelle
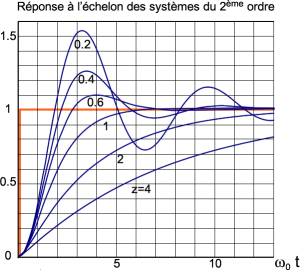
Réponse indicielle
z est le coefficient d'amortissement
Si z>1 la réponse à l'échelon est apériodique de type exponentielle
2 pôles réels : \(p_1=-\omega _0(z-\sqrt{z^2-1})\) et \(p_2=-\omega _0(z+\sqrt{z^2-1})\)
\(S(t)=1-(A\:e^{p_1t}+B\:e^{p_2t})\)
Si z=1 la réponse à l'échelon est critique
1 pôle double : p0=-ω0
\(S(t)=1-((A+Bt)\:e^{-\omega_0t})\)
Si z<1 la réponse à l'échelon est oscillatoire amortie
2 pôles complexes conjugués : \(p_1=-\omega _0(z-j\sqrt{1-z^2})\) et \(p_2=-\omega _0(z+j\sqrt{1-z^2})\)
\(S(t)=1-A\:e^{-z\omega_0t}cos(\omega _0\sqrt{1-z^2}t+\varphi)\)
La méthode consiste à décomposer S(p) en éléments simples, puis d'appliquer la transformée de Laplace inverse
Le temps de réponse le plus faible à un échelon est obtenu pour z=0.7, le temps de réponse à 5% est \(\boxed{tr_{5\%}=\large \frac{3}{\omega_0}}\)