TD N°1

I - Boucles fermées

Question

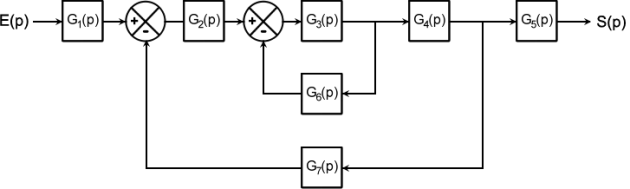
I.1 - Simplifier le schéma fonctionnel ci-dessus en le mettant sous la forme de deux boucles à retours unitaires

Indice

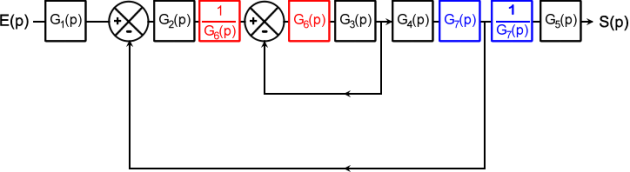
Le bloc G6 (comme le bloc G7) peut être glissé en avant (ou en arrière) mais attention :

Il faudra ajouter un bloc compensateur sur l'entrée + du soustracteur (ou devant le bloc G4 si on le glisse en arrière)

Solution

Ici, arbitrairement le bloc G6 a été glissé vers l'avant, le bloc G7 vers l'arrière

Question

I.2 - À partir du schéma initial, déterminer la fonction de transfert en boucle fermée \(H_{bf}(p)={\frac{S(p)}{E(p)}}\)

Indice

Se souvenir de la formule Hbf=\({\frac{H}{1+KH}}\)

Commencer par simplifier la boucle interne G3 G6

Solution

\(H_{bf}(p)={\frac{G_1(p)G_2(p)G_3(p)G_4(p)G_5(p)}{1+G_3(p)G_6(p)+G_2(p)G_3(p)G_4(p)G_7(p)}}\)

II - Entrées multiples

Question

II.1 - Déduire du schéma fonctionnel ci dessus l'expression littérale de la fonction de transfert en boucle ouverte Hbo(p)

Indice

La FTBO est le rapport de la mesure sur l'erreur en l'absence de perturbation

Solution

\(H_{bo}(p)={\frac{A K_1 K_3 K_2}{p}=\frac{1000}{p}}\)

Question

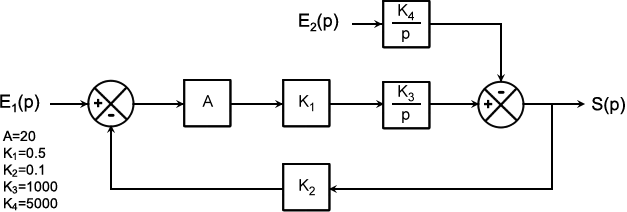
II.2 - En utilisant le théorème de superposition, déterminer S(p) en fonction de E1(p) et E2(p)

Indice

1. E2(p)=0,on calcule la FTBF1 par rapport à E1(p)

2. E1(p)=0, il faut redessiner le schéma avec E2(p) pour consigne, puis calculer la FTBF2

3. On effectue la somme des contributions des 2 FTBF

Solution

\(FTBF_1(p)={\frac{1} {K_2}\frac{1} {(1+\frac{p}{AK_1K_2K_3})}}{=10}{\frac{1}{1+0.001 p}}\)

Schéma pour la FTBF2(p) :

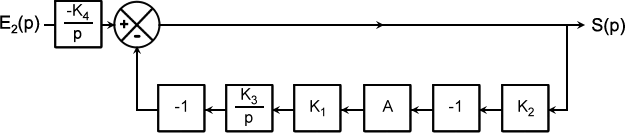
\(FTBF_2(p)={\frac{-K_4} {AK_1K_2K_3}\frac{1} {(1+\frac{p}{AK_1K_2K_3})}}{=-5}{\frac{1}{1+0.001 p}}\)

Question

II.3 - Écrire S(p) sous la forme \(S(p)={\frac{\alpha_1}{1+\mathcal{T} p}}\)E1(p) + \({\frac{\alpha_2}{1+\mathcal{T} p}}\)E2(p)

Calculer α1, α2 et \(\mathcal{T}\)

Indice

La réponse est immédiate

Solution

\(\alpha_1={\frac{1} {K_2}}\) Application numérique : \(\alpha_1=10\)

\(\alpha_2={\frac{-K_4} {AK_1K_2K_3}}\) Application numérique : \(\alpha_2=-5\)

\(\Large \mathcal{T}\)=0.001s=1ms

Question

II.4 - En l'absence de perturbation (E2(p)=0) et en utilisant le théorème de la valeur finale, déterminer S(∞)la valeur finale de S(t) lorsque l'entrée E1(t) est soumise à un échelon d'amplitude 10

Indice

\(\lim\limits_{t \rightarrow +\infty}S(t)=\lim\limits_{p \rightarrow 0}p S(p)\)

Solution

\(\lim\limits_{t \rightarrow +\infty}S(t)=\lim\limits_{p \rightarrow 0}p S(p)=\lim\limits_{p \rightarrow 0}p {\frac{10}{p}\frac{\alpha_1}{1+\mathcal{T} p}=10\alpha_1=100}\)