Fonctions de transfert en boucle fermée et en boucle ouverte
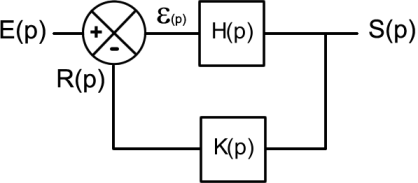
Fonction de transfert en boucle ouverte
C'est le rapport de la mesure sur l'erreur en l'absence de perturbation
\(\boxed {{H_{bo}(p)={\frac{R(p)}{\varepsilon (p)}}{=K(p) H(p)}}}\)
Mais à quoi sert cette FTBO ?
Nous verrons plus tard que son étude permet de prévoir le degré de stabilité de la FTBF, c'est à dire du système bouclé
Fonction de transfert en boucle fermée
Elle détermine la relation entre l'entrée et la sortie d'un système bouclé :
\(\boxed{ H_{bf}(p)={\frac{S(p)}{E(p)}=\frac{H(p)}{1+K(p)H(p)}}}\)
Démonstration
S(p)= H(p) ε(p) = H(p) (E(p)-R(p)) = H(p)(E(p) - K(p)S(p))
Regroupons les termes en S(p) : S(p)+H(p)K(p)S(p)=H(p)E(p)
On factorise S(p) : S(p)(1+H(p)K(p))=H(p)E(p)
Soit \(H(p)={\frac{S(p)}{E(p)}=\frac{H(p)}{1+K(p)H(p)}}\)
Remarque :
Une fonction de transfert doit être exprimée sous la forme de fraction rationnelle en p, c'est à dire comme le quotient de 2 polynômes en p ordonnés selon les puissances croissantes de p
ex. \(H(p){=\frac{a+bp+...}{1+\alpha p+\beta p^2+\gamma p^3+...}}\)